前言

線性判別分析算法的另一種用途是拿來降維，當用在降維時，LDA有另一個別稱--區別分析特徵萃取(Discriminant Analysis Feature Extraction, DAFE)。

降維

LDA的中心思想是將高維的模型樣本投影到最佳鑑別矢量空間，以達到抽取分類信息和壓縮特徵空間維數的效果，投影后保證模式樣本在新的子空間有最大的類間距離和最小的類內距離，即模式在該空間中有最佳的可分離性。

另一種常見的降維技術是PCA，PCA我們在後面的章節會加以介紹。LDA做為降維算法，更多地考慮了標註，即希望投影后不同類別之間數據點的距離更大，同一類別的數據點更緊湊。

在前一章節介紹LDA時，提到它有兩個假設:

1. 樣本數據服從高斯分布
2. 各類的平方差相等。

雖然這些在實際樣本中不一定滿足，但是LDA被證明是非常有效的降維方法，其線性模型對於噪音的魯棒性效果比較好，不容易過擬合。

圖解說明

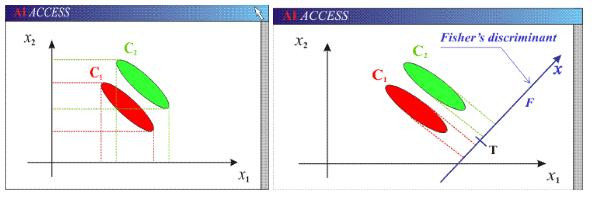
可以看到兩個類別，一個綠色類別，一個紅色類別。左圖是兩個類別的原始數據，現在要求將數據從二維降維到一維。

若我們直接投影將數據到x1軸或者x2軸，不同類別之間會產生重疊，導致分類效果下降。

右圖映射軸是用LDA方法計算得到，可以看到，紅色類別和綠色類別在映射之後，兩者之間的距離是最大的，而且每個類別內部點的離散程度是最小的（或者說聚集程度是最大的）。